Ctrl+K

『なには八ツ橋智恵の渡り』で橋渡り('24.06.05)

『なには八ツ橋智恵の渡り』で橋渡り('24.06.05)#

和算書籍の眞元算法(1845年)に『浪華二十八橋智慧渡』という問題が載っている。 それは、1736年にオイラーが題材とした「ケーニヒスベルクの橋の問題」問題の亜種だ。 つまり、ケーニヒスベルクにある7つの橋を「ひとつの橋を2度通ることなく、全ての橋を渡って、元の場所に帰ってくることができるか？」という問題の変形バージョンである。 オイラーが橋渡り問題を扱った百年後に出された『浪華二十八橋智慧渡』は、オリジナルの問題とは異なる趣向が含まれている。 あるいは、オリジナルの問題の本質を外したことで、別のパズル問題となっているようだ。

_images/day_240605_yatsuhashi_original.png

図 22 オイラーの「ケーニヒスベルクの橋の問題」論文#

今回は、『浪華二十八橋智慧渡』を解くための準備をしてみようと思う。 その題材として使うのは、『浪華二十八橋智慧渡』の簡易版たる『なには八ツ橋智恵の渡り』である。 これは、『浪華二十八橋智慧渡』が扱ったあたりを舞台に、橋の数を8つに減らした単純バージョンだ。

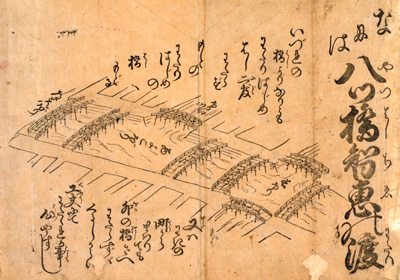
_images/day_240605_yatsuhashi.jpg

図 23 『なには八ツ橋智恵の渡り』#

『なには八ツ橋智恵の渡り』をグラフにしてみる#

まずは、『なには八ツ橋智恵の渡り』をグラフ構造にしてみよう。 後で実際の地名を使うことにして、とりあえずは仮地名でデータを作ってみる。

Hide code cell source 
import numpy as np
import networkx as nx

# c.f. https://medium.com/@victorialandaberry/solving-the-konigsberg-bridge-problem-with-python-914f9f51bb8e
g = nx.MultiGraph() #create an empto Multigraph named G
#add nodes one by one 
g.add_node("難波A")
g.add_node("難波B")
g.add_node("難波C")
g.add_node("難波D")
g.add_node("難波E")
#add edges
g.add_edge("難波A", "難波B")
g.add_edge("難波B", "難波C")
g.add_edge("難波C", "難波E")
g.add_edge("難波A", "難波D")
g.add_edge("難波A", "難波D")
g.add_edge("難波B", "難波D")
g.add_edge("難波B", "難波D")
g.add_edge("難波D", "難波E")
g.add_edge("難波C", "難波D")

print("島の数",  g.number_of_nodes())
print("橋の数", g.number_of_edges())
Hide code cell output 
島の数 5
橋の数 9

作成した『なには八ツ橋智恵の渡り』のグラフ構造を描画してみよう。

Hide code cell source 
from IPython.display import display,SVG

def draw(graph):
    svg = nx.nx_agraph.to_agraph(graph).draw(prog='dot',format='svg')
    display(SVG(svg))

draw(g)
Hide code cell output
_images/4937fd3e7ff7f91d0c450b2bfd811bf1b8332e74b8a551c44b0ebfbb2b9f0222.svg
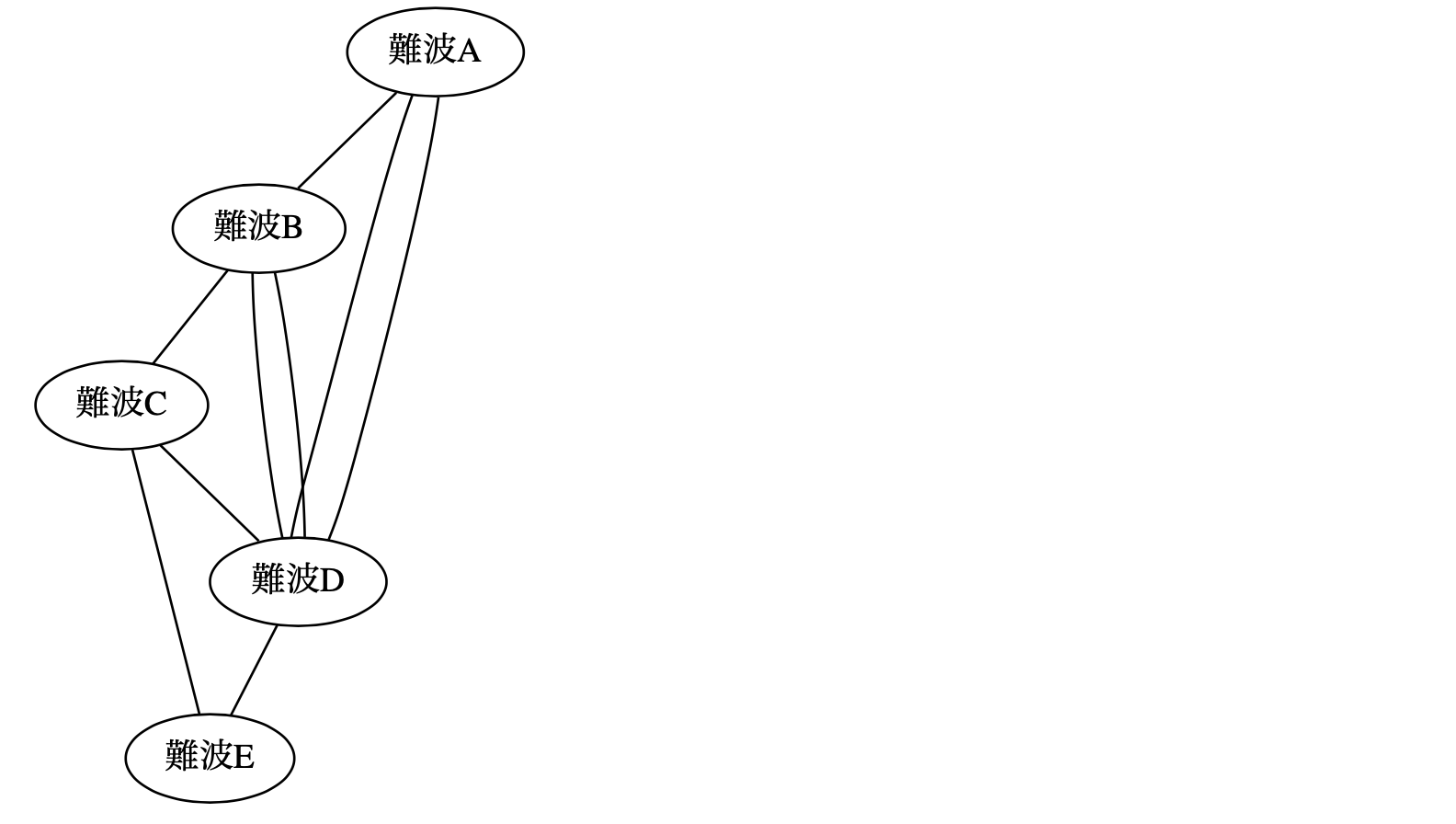
_images/day_240605_yatsuhashi_svg.png

図 24 『なには八ツ橋智恵の渡り』のグラフ構造#

そして、オイラーが1736年に考えた「一筆書きで元の場所に戻れるか」を判定法をPythonコードにして、『なには八ツ橋智恵の渡り』に適用させてみると、答えはこうなる。

Hide code cell source 
def eulerpath(graph):
    odd=0
    a=list(graph.degree(graph.nodes()))
    for i in a:
        if (i[1] % 2) != 0:
            odd+=1
    if odd>0:
        print("一筆書き経路で元の場所に戻ることはできません。")
    else:
        print("一筆書き経路で元の場所に戻ることができます。")

eulerpath(g)

一筆書き経路で元の場所に戻ることはできません。

つまり、オリジナルの「ケーニヒスベルクの橋の問題」と同じ結果が得られる。

ハシを渡りさえしばければワキの町を通り抜けても良い？の謎#

『なには八ツ橋智恵の渡り』には妙な解説文がある。 それは「ハシを渡りさえしばければワキの町を通り抜けても良い」「工夫をすれば渡ることも簡単だ」という一節だ。 この謎について、また眞元算法(1845年)で出題された『浪華二十八橋智慧渡』についても、関連する文章を参考にして、史実や真実の答えに辿り着いてみたいと思う。

_images/day_240605_yatsuhashi_IMG_3321B40D720A-1.jpeg

図 25 『なには八ツ橋智恵の渡り』#

目次