「算法少女(1775年 壺中隠者版)」掲載の円周率計算をしてみる('24.06.10)#
円周率で始まり、円周率で終わる「算法少女」#
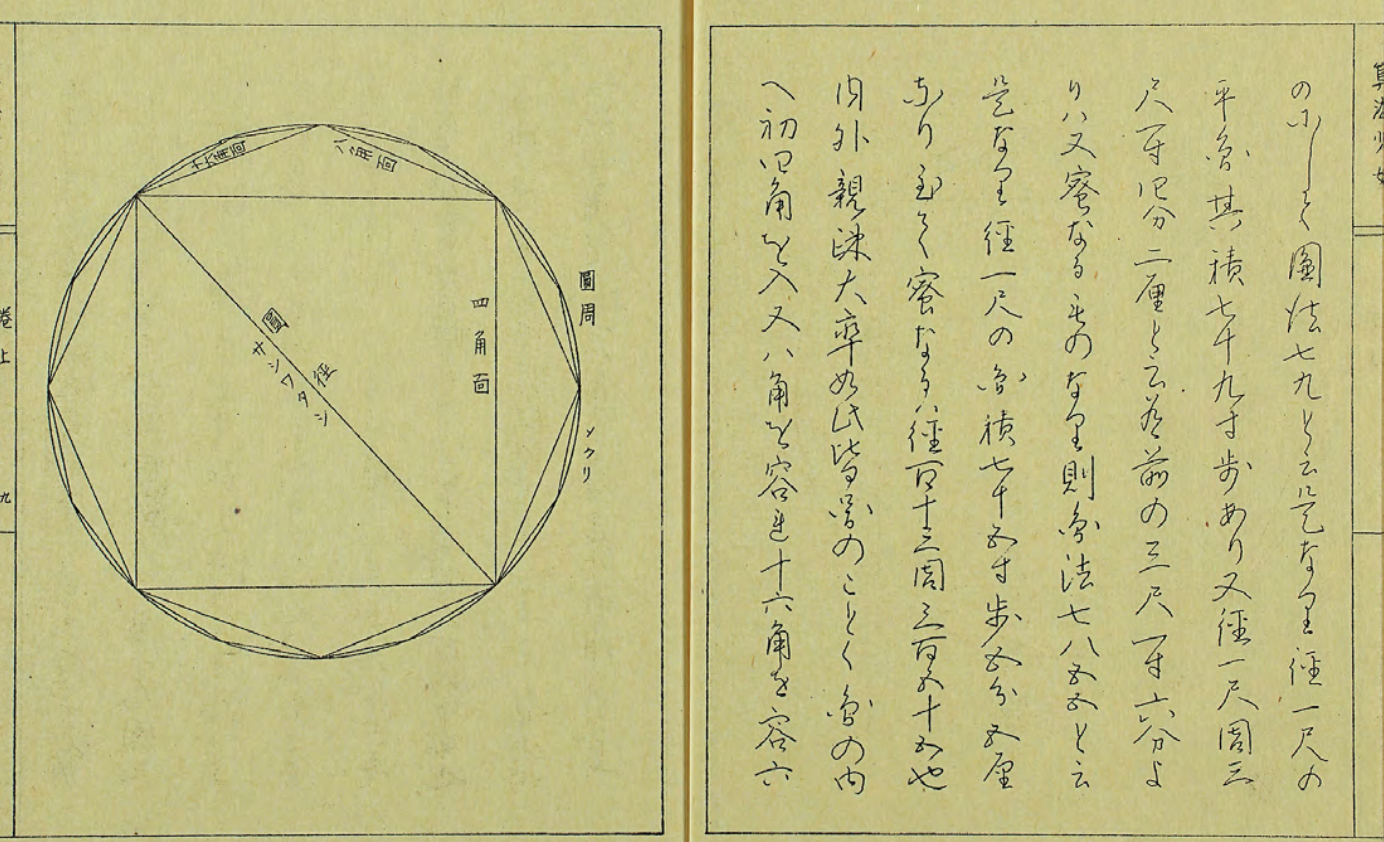
数日前、聖書(列王記, 歴代誌)に書かれている円周率問題を考えた。 1775年、安永4年に書かれた「算法少女」という和算本がある。 書き手は、壺中隠者という名前だが、父親と娘による合作本だと言われている。 この本は、円周率の求め方で書き始められ、円周率計算の起源に関する記載で終わる。 今日は、1775年、安永4年に書かれた「算法少女(壺中隠者版)」に掲載されている計算法を使って、円周率\(\pi\)を計算してみようと思う。
「算法少女(1775年 壺中隠者版)」書かれた円周率級数#
「算法少女(1775年 壺中隠者 版)」に書かれている円周率\(\pi\)の求め方は、このような式だ。
\[ \pi = 3 + 3\times\frac{1^2}{4\times2\times3}+3\times\frac{1^2}{4\times2\times3}\times\frac{2^2}{4\times3\times4}+3\times\frac{1^2}{4\times2\times3}\times\frac{2^2}{4\times3\times4}\times\frac{3^2}{4\times4\times5}\cdots\]
単純に書けば、前項に対して\(\frac{n^2}{4\times(n+1)\times(n+2)}\)という式が掛けられていく級数により円周率を計算することができる、というのが「算法少女(1775年 壺中隠者版)」に書かれている求め方だ※。
試しに10番目までの級数計算をしてみる。 四捨五入すれば、3.14159265といったあたりまでは、有効な値が得られているようだ。
※「算法少女(遠藤寛子1973年版)」では、わかりやすくシンプルにまとめられている
Show code cell source
# n=orderごとの式
def sanpou_pi_element(order):
#print(1+2*(order-1),(1+2*(order-1)+1),(1+2*(order-1)+2))
return (1+2*(order-1))**2 / (4*(1+2*(order-1)+1)*(1+2*(order-1)+2))
# 級数計算
def sanpou_pi(order):
pi=3
last=3
for i in range(order):
current=sanpou_pi_element(i+1)
last=last*current
pi+=last
return pi
# 10 番目までの級数計算をしてみる
sanpou_pi(10)
3.141592646875561
スマホアプリで古今東西の書物を読むと面白い#
最近、さまざまな本を読んでいます。 たとえば、ヘブライ語で書かれた聖書や、江戸時代の崩し文字で書かれた和書本、あるいは聖書(創世記)に関してメルセンヌがラテン語で解説した書物。 全く読み方がわからない書物も、スマホアプリ越しで眺めると、自分が慣れ親しんだ言語として読むことができたりする。 ……というわけで、今日は約250年前の江戸時代の親娘が書いた本を参考にして、Pythonで円周率計算をしてみた。


